최대우도추정법(Maximum Likelihood Estimation)

- 데이터를 바탕으로 모델의 파라미터를 추정하는 방법

- 데이터가 특정 확률 분포에서 생성됨을 가정

이때, 파라미터를 조정하여 데이터가 생성될 확률(우도, likelihood)이

최대가 되는 파라미터 값을 찾는 것이 목표

말로는 이해가 잘 안되는듯해서

동전 던지기 예제로 알아보도록 해요

앞면이 나올 확률이 0.5입니다.

동전 던지기의 결과는 두가지 결과가 나오는 이항 실험(binary experiment)

이기 때문에 베르누이 분포로 모델링 할 수 있습니다.

이때 베르누이 분포에서는 성공 확률 p를 모수(parameter) 로 사용하고

p의 추정값을 구하기 위해서 최대우도추정법을 적용할 수 있습니다.

뭔가 끼워 맞추기 식이 아닌가...?

여튼, 데이터가 발생할 확률을 구하고 모두 곱한 값이 최대가 되도록

모델 파라미터를 조종하는 방법이다 ~!

0.86이란 값이 나왔는데 이게 유의미 한지를 판단하려면 검정이 필요합니다.

신뢰구간 검정을 통해서 파악해보도록 하겠습니다

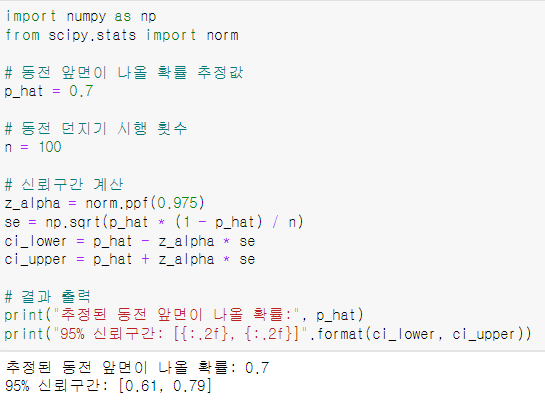
95%의 신뢰구간 안에 있는지를 파악해보았는데

한참 벗어난 수치입니다.

이러한 경우 모형이 잘못되었거나 계산 식에 문제가 있음을 파악할 수 있습니다.

..

..

..

여튼, 데이터가 발생할 확률을 구하고 모두 곱한 값이 최대가 되도록

모델 파라미터를 조종하는 방법이다 ~!

가설검정?

- 어떤 가설이 맞는지 아닌지를 검정하는 통계 방법

귀무가설(null hypothesis) 와 대립가설(alternative hypothesis) 를 설정해야합니다.

예시로는

"제품 A와 제품 B의 성능 차이가 없다" - 귀무가설

"제품 A와 제품B의 성능 차이가 있다" - 대립가설

이제 검정 통계량이 사용됩니다.

귀무가설이 맞는지 틀린지를 판단하는 지표입니다.

또한 검정 통계량은 표본 크기, 표본 편차, 평균값 등의 통계량을 활용하여 계산됩니다.

p-값(p-value)

라는 개념도 등장합니다.

" 귀무가설이 맞다는 가정하에 해당 검정 통계량이 나올 확률 "

간편하게

p-값이 작을수록 귀무가설을 기각하고 대립가설을 채택

간편하게 예시로 알아봅시다.

고객 만족도 조사가 실시되고 있습니다.

이전 조사의 고객 만족도는 80%

최근 조사의 고객 만족도는 75%

귀무가설을 세워보겠습니다

" 이전과 비교하여 고객 만족도는 변화가 없다 "

대립가설은

"이전에 비해 고객 만족도가 떨어졌다 "

위 비율을 비교하기 위해서 Z-검정을 수행합니다.

고객을 1000명이라 두고

귀무가설 = 0.8

대립가설 = 0.75

파이썬 코드로 짜보았습니다

글 하나를 작성하는데 꽤나 오랜 시간이 걸린다. 훗날 이 글을 읽게될 사람들은 작성날짜 역시 확인하며 고충이 따랐음을 글에 대한 플러스 요인에 넣어 주길 바란다.

- 평균, 중앙값, 최빈값

통계를 조금이나마 해본 사람이라면 다들 들어 봤을 법한 단어다.

말 그대로 받아 들이면 된다. 자료들이 어떤 척도로 어느 위치를 '중심'으로 모여있는 지를 안다면

이것을 기준으로 잡아 평균(mean), 중앙값(median), 최빈값(mode) 를 척도로 사용할 수 있다.

- 평균이란?

당신들이 생각하는 그것이 맞다. average

다들 청소년기에 성적 평균 계산을 해 봤을 것이다. 수학+영어+국어/과목수 를 하면 평균 점수가 나온다.

표본 평균과 모평균 역시 위의 예시에선 과목수를 표본의 전체 수로 잡던지 모평균의 전체수로 잡던지 하는 차이이다.

글을 작성하면서도, 공부를 하면서도 매번 느끼지만 굳이 표본,모 이러한 단어들을 익히는 것은 혼란만 더 불어일으킨다고 본다.

- 중앙값이란?

이 역시 당신들이 생각하는 그 값이 맞다. 중앙에 있는 값.

1,2,3,4,5 숫자가 있다면 중앙값은 3.

1,2,3,4,5,6 짝수 숫자가 있다면 중앙에 있는 값의 중앙값. 즉 3과4의 중앙인 3.5

- 최빈값이란?

참고로 글쓴이는 처음에 '빈'을 보고 빈곤함을 떠올려서 가장 없는 숫자? 라는 말도 안되는 생각을 했다.

물론 그것은 아니고 자료 중에서 빈도수가 최대인 값을 의미한다.

여담으로 명목형 자료에서는 평균과 중앙값이 아무런 의미가 없다. 

예시를 들어 보자면

빨강-2 , 주황-5 , 노랑- 7 임의로 색깔에 숫자를 넣었다.

빨강과 주황과 노랑의 평균값을 구하시오 라는 질문에 답을 할 수 있는가?

우리는 빨강과 주황과 노랑이 어떠한 색인지를 알고 있기에 더해서 구할 수 있으나

어떤 색인지 모른다면? 구할 수 없는것이다. 이러한 것이 명목형 자료를 뜻하는 것이고

이런 경우 평균과 중앙값이 전부 의미가 없게 되고 가장 빈도수가 큰 노랑이 대표수가 되는 것이다.

- 사분위수란?

간단하다. 자료를 4개로 나누는 것이다. 1/4 , 2/4 , 3/4 , 4/4. 즉 25%, 50%, 75%, 100% 이다.

분산과 표준편차를 구하는 공식은 위에 첨부 하겠다.

참고로 저자는 " 분산에 루트는 표준편차 " 라는 말을 평생 기억하고 분산만 구하고 있다.

- 변동 계수

쉽게 보지 못하는 것이기도 한데 " 표준편차/평균 x 100% " 이다.

변동성을 평균에 대한 상대적인 값으로 표시한 것인데, 이를 사용하는 이유는

각 다른 회사의 주식 두개의 변동성을 함께 보기 위함? 정도로 파악하면 된다.

변동계수는 표준편차를 평균에 대한 상대적인 값으로 '표준화' 시킨 일종의 표준화된 표준편차이다.

- 피어슨상관계수

 두 숫자형 변수 사이의 선형적 강도를 나타내기 위한 통계량으로 공분산을 각 변수의 표준편차로 나눈 값이다.

그림 없는 표 설명이 가능할까 싶지만 위 글을 찾는 사람들은 가지고 있는 지식에 완성도를 높이기 위해 찾으리라 생각하고

설명이나마 확실하게 해보겠다.

- 도수분포표

학창시절에도 많이 보던 것이다. 자료의 형태를 파악하기 위해 어떤 항목에 어떤 숫자가 있는지를 정리한 것이다.

악보에 어떤 음이 얼만큼 들어갔는지를 예시로 들겠다.

도 1

레 3

미 5

솔 4

합계 13

이런 식인데 가볍게 상대도수 라는것을 구해본다면 어렵게 생각하지 말고 비율을 떠올리면 된다.

단일 갯수/ 전체 갯수 가 공식이다. ' 도 ' 를 예시로 들어 본다면 1/13 = 0.08

전체 악보에서 도가 8%를 차지하고 있다는 것이다. 이해가 되었으면 좋겠다.

- 히스토그램

위키백과에서 복사해온 사진이다. 표본이 너무 적은것 같지만 형태만 파악하면 된다.

위 표를 보면 -1이 100번 , 1이 150번 으로 해석할 수 있다.(무엇에 관한 표본인지를 알 수 없다,,)

이는 '왜도' 라는 것으로 분석할 수 있는데 양의 왜도, 음의 왜도 로 구별할 수 있다.

위 그림 처럼 가운데가 솟은 것은 좌우 대칭 이라고 부른다.

양의 왜도는 왼쪽이 솟아 오르고 오른쪽이 내려간 것이고

음의 왜도는 오른쪽이 솟아 오르고 왼쪽이 내려간 것이라 생각하면 된다.

- 상자 그림

상자 그림 전에 다섯숫자요약을 알아야 한다.

최솟값, 일사분위수, 중앙값, 삼사분위수, 최댓값을 자료 전체의 값으로 요약하는 것이다.

이를 이용해서 그래프를 그리는 것을 상자 수염 그림 이라고 한다.

일사분위 ~ 3사분위로 상자의 길이를 결정한다.(1사분위는 자료의 15% 3사분위는 75% 를 뜻한다)

그 후 중앙값으로 상자의 중앙에 선을 그리고 상자의 대칭성을 파악한다.

상자는 수염 위에 있는데 이 수염의 길이는 최소, 최대 값이다.

- 산점도

짝으로 된 두개의 값을 자료로 나타낼때 사용한다.

위 처럼 점으로 표시된것인데 위키 백과에서 가져온 사진이라 미흡한 부분이 많다..

산점도의 행렬이라는 것도 존재하는데 여기서 점들이 왼쪽 밑에서 오른쪽 위로 ↗ 향한다면 양의 선형관계

왼쪽 위에서 오른쪽 아래로 나열되면 ↘ 음의 선형관계라 할 수 있다.

위 그래프의 경우 양의 선형 관계라고 생각 할 수 있고 차후에 더 설명 하겠다.

- 평행 좌표 그림

쉽게 보기 힘든 그림일 것이다. 잘 사용하지 않는 것으로 알고 있으나 경쟁력이 될 수 있으니 간단하게 설명 하도록 하겠다. 예시로 사람들의 닭, 돼지 ,소고기 섭취량과 같이 3개의 기준점을 잡고 3개를 그래프에 점을 찍고 선을 잇는 것이다.

10명의 사람들로 30개의 점을 찍어서 10개의 선을 만들어 선들의 차이를 보는 과정이라 할 수 있다.

이 글을 읽는 사람의 수준이 얼마나 될지는 모른다.

그러나 분명 통계학의 기초 관해 필요한 것이 있기에 찾아 왔으리라 생각하여 통계학의 역사 라던지는 작성하지 않겠다.

내가 원하는 것은 남들도 원하는 것이라 생각하니 늘 내가 원하던 A to B의 설명을 하고자 한다.

- 통계학은 이익이다.

사회의 이치와 같다. 단순히 합계,평균을 계산하는 일차원적인 수학의 하위 학문이 절대 아니다.

한줄로 요약 하겠다. ' 1000명으로 낸 수치로 3500명을 다뤄서 이익을 낼 수 있어야 한다.' 이것이 정석이다.

정답이 아닌 내가 생각하기에 '정석' 이다. 또한 통계학은 매우 불안정한 학문이다. 100%란 없고 최대치가 99.99999...%에 불과하다는 것을

차후에 알게될 것이다.

- 모집단

통계학의 역사는 몰라도 단어는 알아야 한다. 간단하다. 모집단은 그냥 당신이 조사하고자 하는 '것' 이다.

내가 정석을 논할때 언급한것을 보면 3500명이 모집단이다.

- 표본

이하 동문으로 1000명이 표본이다. 너무 많으니까 일부만 조사하는것이 표본이라 생각하면 된다.

# 조사를 하고자 하는 것은 표본이긴 하지만 결국에는 모집단에 대한 예측이 중요하다. 일부분으로 전체의 정보를 알아낸다.

이것을 우리는 '통계적 추론' 이라 칭한다. ( 표본에서 계산된 통계를 모집단에 대한 정보로 바꾸는 과정)

- 자료

다들 알다시피 통계의 필수 요소다. 자료가 있기 때문에 통계가 있다. 통계학을 공부하는 정도면 단어적인 느낌을 보고 다들 이해하리라 생각한다.

-명목형 자료

이름이나 문자로 나타내는 자료이다. 특징은 순서가 없고 사칙연산이 안된다. 그 옛날 학교 반 친구들 이름의 집단이라 생각하면 된다.

순서를 매길수도 더할수도 없는 자료다.

-순서형 자료

대표적으로 학점이 있다. A B C D F 처럼 문자이지만 '순서'를 매길 수 있는 것들이다. 주의해야 할 점은 사회적인 통념에 의한 순서를 매길 수 있는 것들만 순서형 자료로 취할 수 있다. 내가 생각하기에 순위를 매긴 것을 순서형이라 하면 안된다는 것이다.

-숫자형 자료

말그대로 사칙연산이 가능한 수치로 된 자료다. 수치는 특이하게 ' 5 ' 라고 해서 숫자 5가 아니다. 4.5~5.5 정도의 사이를 나타내게 된다.

보이는 것을 다 믿지 말아야 하고 오차를 생각해야 한다는 뜻이다. 그래서 숫자형 자료는 '범주형 자료' 라고도 한다.

# 여담으로 명목형과 순서형 자료는 질적 자료 또는 비계량적 자료, 숫자형 자료는 양적자료 또는 계량형 자료라고 한다.

이러한 조건들 뿐만 아니라 다른 조건들도 있는데, 시계열과 횡단면 정도가 있다.

- 시계열 자료

말그대로 시간의 변화에 따라 얻는 자료이다. 간단하게 연도별 이자율? 정도를 생각하면 된다.

- 횡단면 자료

어렵다면 어렵게 느낄 수 있는 자료인데, 같은 시차에서의 다른 개체를 분석하는 것이다.

예시로는 A기업과 B기업의 이자율이 차이가 나는 이유가 종목 때문인지 사회 때문인지 등

시간의 변화에 따른 개채를 분석 한다고 생각하면 된다.

줄 글로만 작성하면 가독성이 굉장히 떨어지고 피로해 진다는 것은 충분히 알고 있다.

가볍게 부분 부분을 이해하길 바란다.